Yang Wa HomeArchivesTagsCategoriesGithub
Algorithm
|算法|
Word count: 4k|Reading time: 15 min

动态规划

什么是动态规划

  • 动态规划：类似于数学归纳法，当我们知道n-1的所有情况，那么就可以推出n的情况

动态规划问题求解步骤

  1. dp(状态转移)数组以及其下标的含义
  2. 递推公式
  3. dp数组如何初始化
  4. 遍历顺序
  5. 打印dp数组(检查问题)

动态规划leetcode题目

斐波那契数列

  1. i代表第i个斐波那契数，dp[i]代表第i个斐波那契数的值
  2. dp[i] = dp[i-1] + dp[i-2]
  3. dp[0] = 0 , dp[1] = 1
  4. 从前向后遍历

爬楼梯

  1. i代表第几层，dp[i]代表到达第i层有dp[i]中方法
  2. dp[i] = dp[i-1] + dp[i-2]
  3. dp[1] = 1,dp[2] = 2
  4. 从前向后遍历

不同路径

  1. dp数组及其含义：dp[i][j]代表到达[i][j]的位置有dp[i][j]种方法
  2. 递推公式：每个位置只能由其上边和左边到达，所以dp[i][j] = dp[i-1][j] + dp[i][j-1]
  3. 初始化数组：由于dp[i][0]和dp[0][j]的位置只能由其上边或者左边到达，所以只有一种方法，故将dp[i][0]和dp[0][j]都初始化为1
  4. 遍历顺序：从行到列

股票问题III

  1. dp数组及其含义：由于限制只能买卖两次，所以每一天的状态包含五种，
    • dp[i][0]表示：第i天啥也不干的所剩最多现金
    • dp[i][1]表示：第i天第一次买入股票所剩最多现金
    • dp[i][2]表示：第i天第一次卖出股票(完成第一笔交易)所剩最多现金
    • dp[i][3]表示：第i天第二次买入股票所剩最多现金
    • dp[i][4]表示：第i天第二次卖出股票(完成第二笔交易)所剩最多现金
  2. 递推公式
    • dp[i][0] = dp[i-1][0]，第i天啥也不干，所剩最多现金就是前一天啥也不干留下来的最多现金
    • dp[i][1] = Math.max(dp[i-1][1] , dp[i-1][0]-prices[i]),第i天状态为第一次买入，所剩最大现金为：前一天第一次买入，今天啥也不干或者昨天啥也没干，买入今天股票
    • dp[i][2] = Math.max(dp[i-1][2] , dp[i-1][1]+prices[i]),第i天状态为第一次卖出股票，所剩最大现金为：前一天已经完成第一次交易，今天啥也不干或者昨天第一次买入的状态所剩最大现金加上今天股票的价格
    • dp[i][3] = Math.max(dp[i-1][3] , dp[i-1][2]-prices[i])同理
    • dp[i][4] = Math.max(dp[i-1][4] , dp[i-1][3]-prices[i])同理
  3. 初始化数组：
    • dp[0][0] = 0
    • dp[0][1] = -prices[0]
    • dp[0][2] = 0 第一天买入又卖出，利润为0
    • dp[0][3] = -prices[0] ,第二次买入的状态也为-prices[0],可以理解为第一天买入，卖出，又买入
    • dp[0][4] = 0 第一天买入，卖出，又买入，又卖出，利润为0
  4. 遍历顺序，直接遍历

0-1背包

  1. n种物品，每种物品只有一个

完全背包

  1. n中物品，每种物品有无限个

  2. 零钱兑换 II —求组合数，重复的算一个

  3. 组合总和 Ⅳ — 求排列数，顺序不同则属于不同的答案

    • 在这个问题中，我们有一个目标值（背包的容量）和一组数字（物品）。我们的目标是找出有多少种方式可以使这些数字的和等于目标值。

      1. 先遍历背包，再遍历物品：这种方式对应的是排列数。在这种情况下，我们首先确定背包的容量，然后对于每个容量，我们尝试添加每个物品。这意味着，对于同一组物品，只要它们的添加顺序不同，我们就认为它们是不同的排列。例如，对于目标值 4 和数字 [1, 2, 3]，我们会认为 [1, 2, 1] 和 [2, 1, 1] 是两种不同的方式。
      2. 先遍历物品，再遍历背包：这种方式对应的是组合数。在这种情况下，我们首先确定一个物品，然后尝试将它添加到所有可能的背包中。这意味着，对于同一组物品，无论它们的添加顺序如何，我们都认为它们是同一种组合。例如，对于目标值 4 和数字 [1, 2, 3]，我们会认为 [1, 2, 1] 和 [2, 1, 1] 是同一种方式。

    • 所以，先遍历背包和先遍历物品的区别在于我们如何看待物品的添加顺序：如果我们认为顺序重要，那么就是排列数；如果我们认为顺序不重要，那么就是组合数。

多重背包

  • n种物品，每种物品个数各不相同

0-1背包问题(二维dp数组)

dp数据含义
  • dp[i][j]表示：0到i的物品任取（取或者不取）放进容量为j的背包里价值
递推公式
  • dp[i][j]：
    • 不放物品i，最大价值为dp[i-1][j]，就是不包含物品i的最大价值
    • 放物品i，dp[i-1][j - weight[i]] + value[i]，就是没放物品i之前i- 1个物品在**<减去i物品的重量>**的空间所能产生的最大价值加上物品i的价值。因为要放物品i，所以得所能容纳的重量得减去i的重量
    • 取最大值
初始化dp数组
0-1背包
遍历顺序
  • 两层for循环先遍历物品或者先遍历容量都可以

0-1背包问题(一维数组)

原理
  1. 就是将上一层的数据拷贝到当前层来进行覆盖计算
dp数据含义
  • dp[j]表示：容量为j的背包所能装的最大价值为dp[j]
递推公式
  • dp[j]：
    • 不放物品i，最大价值为dp[j]
    • 放物品i，dp[j - weight[i]] + value[i]
    • 取最大值
初始化dp数组
  • dp[0] = 0,容量为0最大价值就是0
  • 其余初始化为0,不要影响取最大值时的结果
遍历顺序

  • 先遍历物品，在倒序遍历背包容量， 使用倒序是因为使用正序会导致一个物品被重复添加，不符合0-1背包一个物品只能被选择一次的要求

  • 当你在循环中使用正序遍历时，可能会在同一轮循环中多次使用同一个物品。这是因为当计算 dp[j] 时，你可能会使用到 dp[j - weight[i]]，这个值可能在同一轮循环中已经被更新过了。这就意味着你可能会多次使用同一个物品，这违反了 “0-1背包问题” 的规则。

  • 当你使用逆序遍历时，你在计算 dp[j] 时使用的 dp[j - weight[i]] 是上一轮循环的值，这保证了每个物品只被使用一次。

  • 应该使用逆序遍历，而不是正序遍历。

    for(int i = 0; i < 物品数量; i++) {
        for(int j = bigWeight; j >= weight[i]; j--) {
            递推公式
        }
    }

  • 所以当一个物品只能使用一次的时候应该使用逆序遍历背包，可以多次使用时应该正序遍历背包

埃氏筛和欧拉筛

埃氏筛

  1. 埃氏筛全称埃拉托斯特尼筛法，主要用于寻找一定范围内所有的质数
  2. 基本思想：这种方法的基本思想是从 2 开始，首先找到 2 的所有倍数并标记为非质数，然后找到下一个未被标记的数（即质数），再找到它的所有倍数并标记为非质数，以此类推。这种方法的时间复杂度是 O(n log log n)，空间复杂度是 O(n)。

欧拉筛（线性筛）

  1. 区别：欧拉筛在标记倍数时，对其重复标记进行了优化，例如：3的4倍是12，会被标记为合数，2的6倍也是12，也会被标记一次，欧拉筛则是对此处进行了优化，从而提高效率。欧拉筛的时间复杂度是 O(n)。
  2. 实现思路
    1. 新建一个数组status，将除了0,1以外的所有状态置为true，代表默认都是质数
    2. 新建一个数组primes，用来存放所有的质数
    3. 从2开始到n循环，如果是质数，就添加到primes数组中，然后遍历primes，得到其的倍数为合数，在status中置为false
    4. 统计primes的长度即可
  3. 图示

欧拉筛

  1. 解释

    1. 第一步和第二步：从2开始遍历，2为true，代表为质数，加入primes数组中，然后遍历primes，将其与i相乘，得到4，则4为合数，进行标记。
    2. 第三步：i为3，status为true，为质数，加入primes数组中，遍历primes，2 × 3 = 6，3 × 3 = 9，将6和9标记为合数
    3. 第四步：i为4，status为false，为合数，不用加入数组，遍历primes，2 × 4 = 8，将8标记为合数，3 × 4 = 12，应该也将12进行标记，但是如果此时标记了，那么在后面i为6，2 × 6 = 12还是会标记一次，所以这里添加了条件判断  if (i % prime == 0) break;  防止重复标记
    4. 之后的步骤则重复上述步骤，是质数，加入数组，再遍历数组，是合数，直接遍历数组。

  2. 代码

    public int countPrimes(int n) {
        // 记录当前时间
        long start = System.currentTimeMillis();
        if (n < 2) {
            return 0;
        }
        ArrayList<Integer> primes = new ArrayList<>();
        boolean[] status = new boolean[n + 1];
        Arrays.fill(status, true);
        // 0和1不是质数
        status[0] = false;
        status[1] = false;

        for (int i = 2; i < n; i++) {
            // 如果i是质数
            if (status[i]) {
                primes.add(i);
            }
            // 遍历素数集合
            for(int pj : primes) {
                // 得到的合数pj * i出界，结束遍历
                if(pj * i > n) {
                    break;
                }
                status[pj * i] = false;
                // 如果pj是i的最小素因子，结束遍历，防止重复标记合数
                if(i % pj == 0) {
                    break;
                }
            }
        }
        System.out.println(System.currentTimeMillis() - start);
        return primes.size();

回溯法

回溯法三部曲

  • 回溯法中，for循环就是在本层遍历（广度遍历），递归就是向深层次遍历（深度遍历）
function backTracking(参数) {
  if(终止条件) {
      存放结果
    	return
  }
  for(选择本层集合中元素（树结构中的同层元素）) {
   		处理节点
      backTracking(树结构中下一层)
    	回溯，撤销结果
  }
}

回溯法题目

N皇后

  1. 问题描述：N皇后问题，在n*n的棋盘上放置n个皇后，每个皇后的同行，同列，同对角线不能有其他皇后
  2. 树形结构思路：

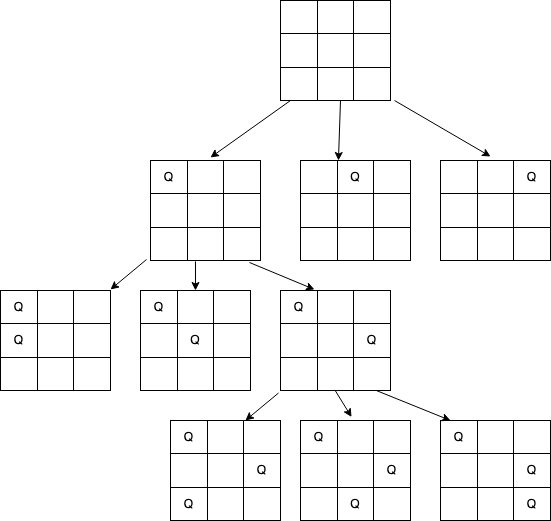
image

  1. 通过上图，根据模板，可以大致写出回溯的代码
//startRow代表当前是第几行
function backTracking(startRow , path) {
  if(startRow === n) result.push(path)
  //向深层次进发
  for(let col = 0; col < n; col++) {
    //如果path[startRow , col]不会被攻击
    if(isvaild) {
      path[startRow][col] = 'Q'
      backtracking(startRow + 1 , path)
      path[startRow][col] = '.'
    }
  }
}

  1. 其余代码包括判断是否在同一行，同一列，同一对角线
/**
 * @param {number} n
 * @return {string[][]}
 */
var solveNQueens = function(n) {
    //初始定义chessBoard为二维数组，fill'.'
    let chessBoard = new Array(n).fill([]).map(() => new Array(n).fill('.'))
    //存储结果的数组
    let result = []
    //回溯函数
    const backTracking = (startRow , chessBoard) => {
        //终止条件
        if(startRow === n) {
            result.push(transformChessBoard(chessBoard))
            return
        }
        //循环本层
        for(let col = 0; col < n; col++) {
            //判断是否会被攻击
            if(isvaild(startRow , col , chessBoard)) {
                //如果不会，就放Q
                chessBoard[startRow][col] = 'Q'
                //向深层遍历
                backTracking(startRow+1 , chessBoard)
               //回溯
                chessBoard[startRow][col] = '.'
            }
        }
    }
    backTracking(0 , chessBoard)
    return result
//判断上方的列，45度方向，135度方向是否有Q，不用判断行因为每次for循环，只会选一行的一个元素，不用判断
function isvaild(row , col , chessBoard) {
    //判断一列中是否有其他Q
    for(let i = 0; i < row; i++){
        if(chessBoard[i][col] === 'Q') return false
    }
    //判断45度方向是否有Q
    for(let i = row - 1 , j = col - 1; i >=0 && j >= 0; i-- , j--) {
        if(chessBoard[i][j] === 'Q') return false
    }
    //判断135度方向是否有Q
    for(let i = row - 1 , j = col + 1; i >=0 && j < n; i-- , j++) {
        if(chessBoard[i][j] === 'Q') return false
    }
    return true
}
//将['Q','.','.','.']转换成"Q..."题目要求的形式
function transformChessBoard(chessBoard) {
        let chessBoardBack = []
        chessBoard.forEach(row => {
            let rowStr = ''
            row.forEach(value => {
                rowStr += value
            })
            chessBoardBack.push(rowStr)
        })

        return chessBoardBack
    }
};

括号生成

  1. 该问题的终止条件：
    • 左括号的数量或者右括号的数量小于零
    • 左括号的数量大于右括号，说明该字符串不符合语法，出现了类似’)()’的情况
    • 左括号和右括号的数量为0，说明正常配对完毕，可以放入结果中
var generateParenthesis = function(n) {
    let result = []
    let path = []
    const backTracking = (right , left , path) => {
        if(left < 0 || right < 0) return
        if(left > right) return
        if(left === 0 && right === 0) {
            result.push(path.join(''))
            return
        }
        path.push('(')
        backTracking(right , left - 1 , [...path])
        path.pop()

        path.push(')')
        backTracking(right - 1 , left , [...path])
        path.pop()
    }
    backTracking(n,n,path)
    return result
};

字典树

何为字典树

  1. 字典树（Trie Tree）：一般称为前缀树，是一种用于存储字符串的数据结构，主要用于快速检索字符串。

字典树题目

实现 Trie (前缀树)

  1. 代码

    var Trie = function () {
        this.children = [];
        this.isLast = false;
    };

    Trie.prototype.insert = function (word) {
        /** 将this赋值给node，当需要切换到下个节点时直接赋值给node即可
         ** 不能直接赋值给this.children,this.children = this.children[index].children;
         ** 需要这样写： node = node.children[index];
         **/
        let node = this;
        let n = word.length;
        for (let i = 0; i < n; i++) {
            const index = word[i].charCodeAt(0) - 'a'.charCodeAt(0);
            if (node.children[index] == null) {
                node.children[index] = new Trie();
            }
            node = node.children[index];
        }
        node.isLast = true;
    };

    Trie.prototype.search = function (word) {
        let n = word.length;
        let node = this;
        for (let i = 0; i < n; i++) {
            const index = word[i].charCodeAt(0) - 'a'.charCodeAt(0);
            if (node.children[index] == null) {
                return false;
            }
            node = node.children[index];
        }
        return node.isLast;
    };

    Trie.prototype.startsWith = function (prefix) {
        let node = this;
        let n = prefix.length;
        for (let i = 0; i < n; i++) {
            const index = prefix[i].charCodeAt(0) - 'a'.charCodeAt(0);
            if (node.children[index] == null) {
                return false;
            }
            node = node.children[index];
        }
        return true;
    };

单词的压缩编码

  1. 该问题需要寻找是否是公共后缀，所以需要倒叙插入字典树

  2. 代码

    function minimumLengthEncoding(words: string[]): number {
        let root = new TrieNode();
        let map = new Map();
        let res = 0;
        for(let word of words) {
            let cur = root;
            // 这里需要从尾部插入
            for(let i = word.length - 1; i >= 0; i--) {
                let c = word.charAt(i);
                cur = cur.get(c);
            }
            map.set(cur, word.length + 1)
        }

        for(const [key ,value] of map.entries()) {
            if(key.isEnd) {
                res += value;
            }
        }
        return res;
    };

    class TrieNode {
      children: Array<TrieNode> ;
      isEnd: boolean;
      
      constructor() {
        this.children = new Array<TrieNode>();
        this.isEnd = true;
      }

      get(c: string): TrieNode { 
        const index = c.charCodeAt(0) - 'a'.charCodeAt(0);
        if (this.children[index] == null) {
          this.children[index] = new TrieNode();
          this.isEnd = false;
        }
        return this.children[index];
      }
      
    }

单词替换

  1. 代码

    class Solution {
        public String replaceWords(List<String> dictionary, String sentence) {
            TrieNode root = new TrieNode();
            for (int i = 0; i < dictionary.size(); i++) {
                TrieNode cur = root;
                String word = dictionary.get(i);
                for (int j = 0; j < word.length(); j++) {
                    char c = word.charAt(j);
                    cur = cur.insert(c);
                }
                cur.isRoot = true;
            }
            String[] sen = sentence.split(" ");
            for (int i = 0; i < sen.length; i++) {
                TrieNode cur = root;
                sen[i] = cur.get(sen[i]);
            }
            return String.join(" ", sen);
        }
    }

    class TrieNode {
        TrieNode[] children;
        boolean isLast;
        boolean isRoot;

        public TrieNode() {
            this.children = new TrieNode[26];
            this.isLast = true;
            this.isRoot = false;
        }

        public TrieNode insert(char c) {
            int index = c - 'a';
            if (this.children[index] == null) {
                this.children[index] = new TrieNode();
                this.isLast = false;
            }
            return this.children[index];
        }

        public String get(String sen) {
            TrieNode node = this;
            String temp = "";
            for (int j = 0; j < sen.length(); j++) {
                char c = sen.charAt(j);
                int index = c - 'a';
                if (node.children[index] == null) {
                    return sen;
                }
                temp += c;
                if (node.children[index].isRoot) {
                    return temp;
                }
                node = node.children[index];
            }
            return temp;
        }
    }
Author: Yang Wa
Link: https://blog.wxywxy.cn/2024/09/24/Algorithm/
Copyright Notice: All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.
算法